Внеклассное мероприятие «Музыка, математика и информатика»
Интегрированный урок математики в 6 классе
Гришко Елена Михайловна, учитель математики МБОУ «СОШ№4» г.Красноперекопска, республика Крым
Цель урока:
— определить взаимосвязи математики и музыки;
— способствовать формированию нового взгляда на мир;
— формировать потребность поиска ответов на возникающие вопросы;
— развивать творческие способности учащихся, ассоциативное мышление, воображение и фантазию;
— воспитывать открытую, свободную личность, способную к познанию, активному действию.
Оборудование: компьютер, проектор, презентация.
План урока:
- Организационный момент.(1 мин).
- Мотивация.(2 мин).
- Психологический настрой.(1 мин).
- Историческая справка (компьютерная презентация, 10 мин).
- Противоположности в музыке и в математике. (4 мин).
- Актуализация опорных знаний.(5 мин).
- Длительность нот и обыкновенные дроби. (7 мин).
- Ритмическая разминка. (1 мин).
- Решение задачи. (4 мин).
- Цифровая музыка (компьютерная презентация). (2 мин).
- Тестовый контроль знаний с помощью компьютера.(5 мин).
- Оценивание учащихся.(1 мин).
- Подведение итогов урока.(2 мин).
Ход урока:
- Организационный момент.
Учитель. Здравствуйте, ребята. Тема нашего урока «Музыка, математика и информатика». Сегодня мы будем говорить о музыке и о математике.
- Постановка цели урока.
Учитель. Как вы думаете, какая цель нашего урока? (Понять, как связаны музыка с математикой?)
Слайд 2
Учитель. Верно, определить взаимосвязи между музыкой и математикой.
- Психологический настрой.
Учитель. Музыка бывает мажорная и минорная, а это значит, и настроение у нас сегодня должно быть только мажорное.
- Историческая справка (компьютерная презентация).
Слайд 3.
Одновременно звучит музыка Л. Бетховена — фортепианная багатель К.Элизе.
Учитель. Математика и музыка – два полюса человеческой культуры. Математика – это наука, связанная со строгим логическим мышлением, упорядоченным и неограниченным пространством чисел. Музыка – это искусство, связанное с воображением, фантазией, с таинственным и безграничным миром звуков. Музыка действует на чувства, душу, математика – на разум. Казалось бы, какая между ними связь? Однако связь математики и музыки обусловлена как исторически, так и внутренне, несмотря на то, что математика – самая абстрактная из наук, а музыка – наиболее отвлеченный вид искусства.

Учитель. Основоположником теории музыки был великий древнегреческий математик Пифагор (Vl в. до н.э).
Слайд 4
Пифагор основал научную и эзотерическую закрытую школу, в которой преподавались различные математические дисциплины. Пифагорейцы, так называли себя его ученики, занимались астрономией, гармонией (теорией музыки), геометрией, арифметикой и пытались выразить все законы вселенной с помощью чисел.
Слайд 5
Известно открытие Пифагора в области музыки. Необычность его в том, что сочетание звуков, издаваемых струнами, наиболее благозвучно, если длины струн музыкального инструмента находятся в правильном численном отношении друг другу.
Слайд 6
Для воплощения своего открытия Пифагор использовал монохорд – изобретение, состоящее из одной струны, натянутой между зажимами и снабженное подвижными ладами. Под струной на верхней крышке ученый начертил шкалу, с помощью которой можно было делить струну на части.
Слайд 7
Когда Пифагор передвигал перекладины, прижимая их к заранее размеченным точкам, звучали различные музыкальные интервалы. Сравнив высоту целой струны и ее половинки, он был поражен: струна, которая была вдвое корче, звучала значительно выше, но тем же тоном, что и целая струна. При этом тон целой струны и тон ее половинки как бы сливались воедино, издавая чистое согласное созвучие.
Слайд 8
Пифагор обнаружил, что приятные слуху созвучия – консонансы — получаются лишь в том случае, когда длины струн относятся как целые числа первоначальной четверки, т. е. как 1:2, 2:3, 3:4.
Слайд 9
Пифагор разделил струну на три, четыре, пять равных частей, при этом он получал разные по высоте звуки.
Слайды 10-11
Эти звуки-тоны Пифагор расположил по высоте этакими ступеньками звуковой лесенки, и у древнего математика получилось, что внутри октавы, между ее верхним и нижним звуками, уместилось 8 звуков ступенек. Гораздо позднее расстояние между нижним и верхним тонами абсолютного созвучия стали называть октавой, что на латинском языке означает «восьмая». Впоследствии 8 звуков, получившие имена ДО-РЕ-МИ-ФА-СОЛЬ-ЛЯ-СИ и снова ДО, обязательно повторяются внутри каждой октавы. Этот ряд – звукоряд – позже стал называться Пифагоровым строем или Пифагоровым звукорядом.
Слайд 12
Итак, один из законов, который лег в основу Пифагорейской музыки: две звучащие струны определяют консонанс, когда их длины относятся как целые числа, образующие треугольное число 10=1+2+3+4, т. е. как 1:2, 2:3, 3:4.
Слайд 13
XVII век ознаменовался новыми открытиями в области математики. В 1614 году опубликованы таблицы логарифмов. Их автор – шотландец Д.Непер. Благодаря расчетам с помощью логарифмов стало ясно, что музыкальная шкала должна быть разделена на 12 равных частей. И XVIII век открыл новые страницы в истории музыки. В 1700 г. немецкий органист Андреас Веркмейстер осуществил гениальное решение: сохранив октаву, он разделил ее на 12 равных частей. Настроенные им органы зазвучали в равномерно-темперированном строе (темперация от лат. соразмерность). Величайший немецкий композитор Иоганн Себастьян Бах первым продемонстрировал достоинства новой музыкальной системы, написав «Хорошо темперированный клавир», состоящий из 12 мажорных и 12 минорных произведений (клавир – старинное название клавесина).
История создания равномерной темперации еще раз свидетельствует о том, как тесно переплетаются судьбы математики и музыки. Рождение нового музыкального строя не могло произойти без изобретения логарифмов. Логарифмы стали своеобразной «алгеброй гармонии», на которой выросла темперация.
- Противоположности в музыке и в математике.
Учитель. Мы с вами сегодня попробуем найти общие точки соприкосновения точной науки математики и изящного искусства музыки. Первый раздел нашего исследования – противоположности.
Противоположности в музыке.
Учитель. В музыке есть яркие противоположности – мажорный лад и минорный лад.
Слайд 14
Лад – объединение звуков, различных по высоте и тяготеющих друг к другу.
Мажорный лад сияет
Блестящим, ярким светом,
И разным он бывает –
Но только ясным, светлым. (И.С.Бах – Шутка из оркестровой сюиты №2.)
Слайд 15
А музыка в миноре
Звучит не так блестяще –
То жалобно, то споря,
То нежно и просящее. (Ф.Шопен – Вальс си-минор)
Противоположности в математике.
- Какие числа мы называем противоположными?
- Приведите пример противоположных чисел.
- Актуализация опорных знаний учащихся.
Учитель. Второй раздел нашего исследования – длительность нот и обыкновенные дроби. Чтобы продолжить наши поиски, мы должны вспомнить правила сложения, вычитания, умножения и деления для обыкновенных дробей.
Фронтальный опрос.
- Как складывают и вычитают обыкновенные дроби с разными знаменателями?
- Как умножают обыкновенные дроби?
- Как выполняют действие деления обыкновенных дробей?
Вычислите устно: Слайд 18 (Устный счет)
- Длительность нот.
Слайд 17
Учитель. Оказывается, длительности музыкальных нот заимствовали свои названия у обыкновенных дробей.
Ученик 1. Рядом с нами круглый год
Чудо-музыка живет.
Сколько звуков в ней услышишь:
То пониже, то повыше,
То потише, то погромче,
То длиннее, то короче…
О последних мы как раз
И поговорим сейчас.
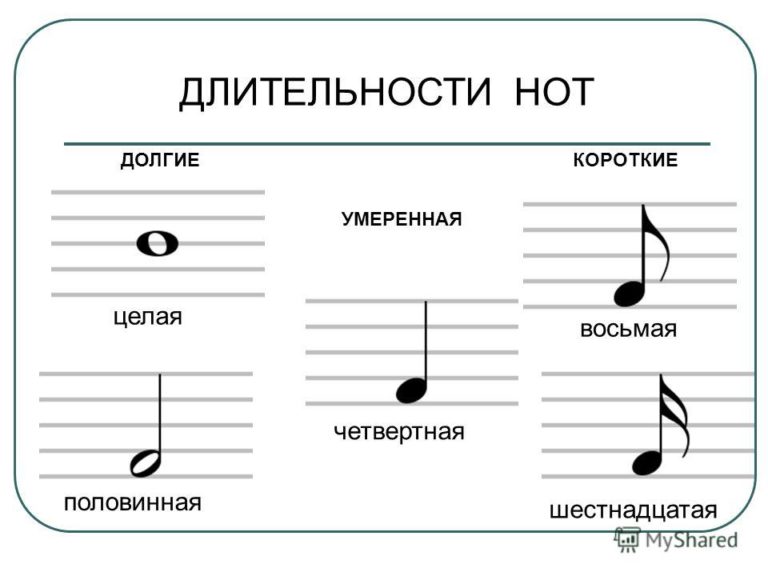
Ученик 2. Эта нота целая,
Круглая и белая,
Самая солидная
И очень-очень длинная.
Эта половинная,
Тоже нота длинная,
У нее овал белый похожа она на целую.
Ноту мы нарисовали:
Штиль с закрашенным овалом.
Имя ноты каждый знает:
Эта нота – четвертная.
К четвертной дорисовали
Хвостик – и восьмой ее назвали.
Эта нота, между прочим,
Вдвое четвертной короче.
Как подружки озорные
Неразлучны меж собой,
Взявшись за руки, восьмые
Часто бегают гурьбой.
Ну а хвостиков, смотри,
Может быть один, два, три…
Мы их там нарисовали,
Где закрашены овалы.
Слайд 18
Учитель: Шестнадцатая, восьмая, четвертная, половинная, целая нота. Названия длительности служат одновременно и названиями чисел. Нетрудно понять, почему длительности музыкальных нот заимствовали свои названия у дробей. Мы видим, что длительности получаются так же, как и дроби: они возникают при делении целой на равные доли. Поэтому длительность можно подсчитывать, как дробные числа, например:
Слайд 19
С помощью чисел это можно записать так:
Рассмотрим схему длительности нот. Установим связи между длительностями нот. Ответьте на вопросы:
- Длительность какой ноты мы получим, если пропоем две половинные? Две четвертные? Две восьмые? Две шестнадцатые?
- Найдите сумму дробей:
Слайд 20
Решите ритмические примеры:
- Музыкальная разминка.
Учитель. Давайте организуем «ритмический оркестр». Каждый из вас будет отстукивать только свою длительность. (Cчитаю до двадцати, а ученики отхлопывают каждый свою длительность: целую, половинную и четвертную)
- Решение задачи.
Слайд 21
Задача. Известно 80 музыкальных произведений, написанных Бетховеном. Из них 32 сонаты и 9 симфоний. Сколько процентов составляют 32 сонаты и 9 симфоний от всех музыкальных произведений, написанных композитором?
Решение.
(32+9):80·100=51,25% — составляют сонаты и симфонии от всех произведений, написанных Бетховеном (Ответ: 51,25%)
- Цифровая музыка (компьютерная презентация).
Слайды 22-24
Учитель. На протяжении многих веков судьбы музыки и математики переплетались, а сегодня музыка вплетена в информатику. Благодаря математике музыку удалось «ввести» в компьютер. Такую музыку называют цифровой. Компьютер оперирует с данными в цифровом виде. Как же происходит преобразование аналогового сигнала в цифровой (оцифровка звука)?
Слайд 25
Звук распространяется в виде волн. В каждом промежутке времени измеряется значение амплитуды сигнала, записывается и сохраняется в виде чисел.
Слайд 26
Таким образом, оцифровка звука – это фиксация амплитуды сигнала через определенные промежутки времени и регистрация полученных значений амплитуды в виде округленных цифровых значений. Очевидно, чем чаще мы будем делать замеры амплитуды и чем меньше будем округлять полученные данные, тем более точное значение сигнала в цифровой форме мы получим. В последнее время возможности мультимедийного оборудования значительно возросли.
Слайды 27-28
Источником цифрового звука являются: мобильный телефон, флешка, лазерный диск, компьютерный плеер, цифровой телевизор.
Дополнительный материал.
Пифагорейцы известны в истории эстетики благодаря еще одной теории. Она также была связана с музыкой, но имела иной характер. Если первая теория, как мы убедились, была построена на математических пропорциях, то вторая провозглашала музыку силой, способной воздействовать на душу. Хорошая музыка может улучшить душу, а плохая — испортить ее. Такое музыкальное действие греки называли психагогией, или управление душами. Одним из тех, кто первым научно объяснил целебный эффект музыки, был… Пифагор, утверждавший, что музыка подчиняется высшему закону (математике) и вследствие этого восстанавливает в организме человека гармонию. Однажды Пифагору даже удалось с помощью музыки успокоить разгневанного мужа, в припадке ревности пытающегося сжечь дом, в то время как никто из родных не мог его остановить. А древнегреческий врач Гиппократ лечил музыкой бессонницу и эпилепсию.
В начале XX века известный психоневролог Владимир Михайлович Бехтерев начал изучать влияние музыки на организм человека. Ученый пришел к выводу, что музыка может избавлять от усталости и заряжать человека энергией, положительно влиять на систему кровообращения и дыхания. Академик Бехтерев считал, что матери недаром поют своим малышам. «Без колыбельной вообще невозможно полноценное развитие ребенка», —писал ученый.
Полчаса классической музыки в день обязательны для всех детей американского штата Флорида – так велит принятый там уже шесть лет назад закон № 660, иначе называемый Beethoven’s Babies Bill. Законодатели штата уверены: музыка не только помогает малышам заснуть в «тихий час», но и способствует гармоничному развитию мозговой деятельности ребенка. Во Франции благотворное влияние музыки используют в некоторых столичных детских больницах
- Проведение компьютерного тестирования учащихся по теме урока «Музыка и математика».
Слайды 29-39
Слайд 40
Ключи к тесту. 1) 0; 2) -17; 3) 5/8; 4)1/12; 5)Такт; 6)Монохорд; 7)Хормейстер; 8) Штиль; 9) Моцарт; 10) Витас.
- 1-а;
- 2-в;
- 3-д;
- 4-б;
- 5-в;
- 6-г;
- 7-а;
- 8-а;
- 9-в;
- 10-б.
- Оценивание учащихся.
- Подведение итогов урока.
Учитель. Итак, цель нашего урока — «Определить взаимосвязь музыки и математики». Где прослеживаются математические законы в музыке?
Ответ: в нотной записи музыкальных произведений; при настройке музыкальных инструментов; в создании цифровой музыки; математические пропорции могут быть применены к описанию построения некоторых музыкальных фрагментов.
Учитель. Ученые всего мира изучают поистине интереснейшую проблему взаимосвязи математики и музыки. Выводы, которые можно сделать, исходя из результатов их деятельности: музыку можно описать, но нельзя объяснить математикой, хотя математика неизбежно диктует музыке свои законы как относительно нотной записи, так и относительно построения.
- Задание на дом (задание по карточкам).
Учитель. Урок окончен. Спасибо.
