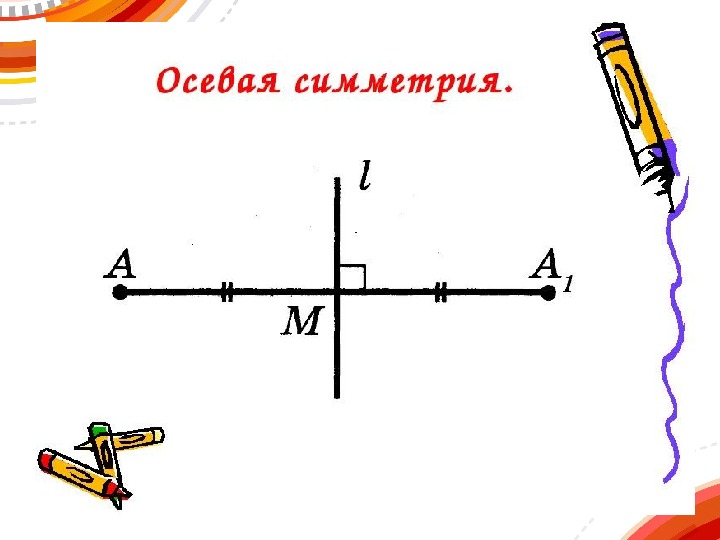
Осевая симметрия
Конспект урока по алгебре в 9 классе
Автор: Азиза Исламовна БАБАДЖАНОВА, МБОУ «Лицей № 22», г. Иваново
Тип урока: урок усвоения нового знания.
Цели урока:
- дать представление о понятии осевой симметрии;
- доказать, является ли осевая симметрия движением;
- показать учащимся связь математики с другими областями науки, искусством и реальной действительностью.
Образовательная:
- познакомить с понятием симметрии;
- сформировать понятие «симметричные фигуры», «симметричные предметы»;
- формировать способность проводить ось симметрии;
- формировать способность определять симметричные предметы в окружающем мире;
- строить симметрию фигур, относительно оси симметрии;
- учить применять симметрию в практической деятельности.
Развивающая:
- развивать логическое мышление, внимание, воображение;
- коммуникативные качества;
- практические умения;
- навыки рефлексии (самоанализ деятельности).
Воспитательная:
- воспитывать устойчивый интерес к изучению математики;
- воспитывать взаимную вежливость, аккуратность;
- расширять эстетические представления о мире (понятие красоты, совершенства, гармонии).
На уроке использована фронтальная работа, индивидуальная работа.
Методы обучения: наглядный, словесный, практический, частично-поисковый, репродуктивный.
Оборудование и пособия: компьютер, проектор, презентация к уроку.
Ход урока:
- Организационный этап.
Учитель организует учащихся для работы на уроке; проверяет готовность класса; сообщает тему, записанную на доске; говорит о важности данной темы, о связи темы с ранее изученным материалом; цели урока.
- Актуализация опорных знаний, умений и навыков.
Опрос учителя по теории:
- Что такое преобразование плоскости?
- Какое преобразование плоскости называется движением?
- Всякое ли преобразование плоскости является движением? Почему?
На доске заготовлены два чертежа.
- а) Постройте точку, симметричную данной, относительно прямой.
- б) Если рассмотреть ось симметрии под наклоном, поменяется ли принцип построения?
Ученики с места отвечают на поставленные вопросы.
- Изучение нового материала.
- Что же такое осевая симметрия?
- Какие условия должны выполняться?
Sl(A) = Aꞌ, где А-прообраз, Aꞌ — образ
- Является ли движением осевая симметрия? Докажите это.
Давайте возьмем еще одну точку и также построим симметричную ей относительно оси. И докажем, что АВ= Aꞌ Вꞌ
- Какая фигура получилась? Как мы докажем, что это правильная трапеция?
- Итак, как докажем, что АВ= Aꞌ Вꞌ
- Презентация.
Давайте рассмотрим картинки на слайде. Например листок.
- Можем ли мы провести ось симметрии?
- Подумайте, какие геометрические фигуры имеют одну ось симметрии? Две? Более двух?
- Также симметрия встречается и в архитектуре.
- А какие печатные буквы русского алфавита имеют ось симметрии? Какие они и сколько их может быть?
- Закрепление, первичная проверка изученного материала.
Задание 1. Построить фигуру, симметричную данной, относительно оси. Могут ли некоторые точки при осевой симметрии оставаться неподвижными? Какие это точки?
Задание 2. Построить фигуру, симметричную данной, относительно оси.
Ученики выполняют построения у себя в тетрадях, кто-то один у доски с объяснением. Запись: Sl(AВСD) = AꞌВꞌСꞌDꞌ Могут. Те, которые лежат на самой оси симметрии. Запись: Sl(AВС) = AꞌВꞌСꞌ
- Домашнее задание.
- Придумать фигуру и построить ей симметричную, относительно оси.
- Придумать слова, имеющие вертикальную и горизонтальную оси симметрии.
- Подведение итогов урока.
- О чем мы сегодня с вами говорили?
- Что же такое осевая симметрия?
- Что должно выполняться?
- Является ли движением осевая симметрия?
- Как строится симметрия?
- Рефлексия.
- Если вы считаете, что поняли тему сегодняшнего урока, то хлопните три раза в ладоши.
- Если вы считаете, что недостаточно усвоили материал, то хлопните всего один раз.
- Если вы считаете, что не поняли тему сегодняшнего урока, то хлопать не надо.
Вы аплодировали себе и своим новым знаниям. Спасибо за урок.
